במתמטיקה, הכלל האמפירי אומר כי במערך נתונים רגיל, כמעט כל נתון נתונים ייפול בתוך שלוש סטיות תקן סטיית תקן מנקודת מבט סטטיסטית, סטיית התקן של מערך נתונים היא מדד לגודל הסטיות בין הערכים. מהתצפיות הכלולות בממוצע. הממוצע הוא הממוצע של כל המספרים בתוך הסט.
הכלל האמפירי מכונה גם כלל שלושת הסיגמא או הכלל 68-95-99.7 משום:
- בתוך סטיית התקן הראשונה מהממוצע, 68% מכלל הנתונים נשענים
- 95% מכלל הנתונים ייפלו בשתי סטיות תקן
- כמעט כל הנתונים - 99.7% - נופלים בתוך שלוש סטיות תקן (.3% שנותרו משמשים לחשבונם של חריגים, שקיימים כמעט בכל מערך נתונים)
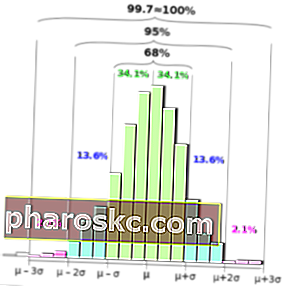
הפצה רגילה
הכלל האמפירי נוצר מכיוון שאותה צורה של עקומות תפוצה המשיכה להופיע שוב ושוב לסטטיסטיקאים. הכלל האמפירי חל על התפלגות נורמלית. בהתפלגות נורמלית כמעט כל הנתונים נופלים בתוך שלוש סטיות תקן של הממוצע. הממוצע הממוצע הוא מושג חיוני במתמטיקה ובסטטיסטיקה. באופן כללי, ממוצע מתייחס לממוצע או לערך הנפוץ ביותר באוסף של, מצב וחציון שווים כולם.
- הממוצע הוא הממוצע של כל המספרים בערכת הנתונים.
- המצב הוא המספר החוזר בתדירות הגבוהה ביותר בתוך מערך הנתונים.
- החציון הוא ערך הפיזור בין המספרים הגבוהים והנמוכים ביותר בתוך הסט.
המשמעות היא שהממוצע, המצב וחציון החציון החציוני הוא מדד סטטיסטי הקובע את הערך האמצעי של מערך נתונים המופיע בסדר עולה (כלומר, מהערך הקטן ביותר לגדול ביותר). החציון אמור לכלול במרכז מערך הנתונים. מחצית מהנתונים צריכים להיות בקצה העליון של הסט, והחצי השני למטה.
קביעת סטיית התקן
הכלל האמפירי שימושי במיוחד לחיזוי תוצאות בתוך מערך נתונים. ראשית, יש לחשב את סטיית התקן. הנוסחה מוצגת להלן:
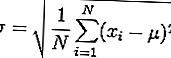
הנוסחה המסובכת לעיל מתפרקת באופן הבא:
- קבע את ממוצע מערך הנתונים, שהוא סך כל מערך הנתונים, חלקי כמות המספרים.
- עבור כל מספר בערכה, חיסר את הממוצע ואז רבע את המספר המתקבל.
- בעזרת הערכים בריבוע, קבע את הממוצע עבור כל אחד מהם.
- מצא את השורש הריבועי של האמצעים שחושב בשלב 3.
זוהי סטיית התקן בין שלושת האחוזים הראשוניים של ההתפלגות הנורמלית, שבתוכם רוב הנתונים בערכה צריכים ליפול, לא כולל אחוז מינורי לחריגים.
שימוש בשלטון האמפירי
כאמור לעיל, הכלל האמפירי שימושי במיוחד לחיזוי תוצאות בתוך מערך נתונים. סטטיסטית, לאחר קביעת סטיית התקן, ניתן בקלות לקבוע את ערכת הנתונים לכלל האמפירי, ולהראות היכן פיסות הנתונים טמונות בהתפלגות.
חיזוי חיזוי חיזוי מתייחס לפרקטיקה של חיזוי מה יקרה בעתיד תוך התחשבות באירועים בעבר ובהווה. בעיקרון, זהו כלי לקבלת החלטות המסייע לעסקים להתמודד עם השפעת חוסר הוודאות של העתיד על ידי בחינת נתונים ומגמות היסטוריות. אפשרי מכיוון שגם בלי לדעת את כל הנתונים הספציפיים, ניתן לבצע תחזיות היכן הנתונים ייפלו בתוך הסט, בהתבסס על התכתיבים 68%, 95% ו 99.7% המראים היכן כל הנתונים צריכים לנוח.
ברוב המקרים, הכלל האמפירי הוא שימוש ראשוני בכדי לסייע בקביעת התוצאות כאשר לא כל הנתונים זמינים. זה מאפשר לסטטיסטיקאים - או לומדים את הנתונים - לקבל תובנה היכן הנתונים ייפלו, ברגע שהכל יהיה זמין. הכלל האמפירי מסייע גם לבחון עד כמה מערך נתונים הוא נורמלי. אם הנתונים אינם עומדים בכלל האמפירי, הרי שלא מדובר בהתפלגות נורמלית ויש לחשבם בהתאם.
קריאות קשורות
מימון היא הספקית הרשמית של הסמכת ה- FMVA® ™ FMVA® העולמית של מודלים פיננסיים למודלים והערכה פיננסיים. הצטרפו ל -350,600 סטודנטים ועובדים בחברות כמו אמזון, ג'יי.פי מורגן ופרארי, שנועדו לעזור לכל אחד להיות אנליסט פיננסי ברמה עולמית . כדי להמשיך ללמוד ולקדם את הקריירה שלך, משאבי האוצר הנוספים להלן יהיו שימושיים:
- נטייה מרכזית נטייה מרכזית נטייה מרכזית היא סיכום תיאורי של מערך נתונים באמצעות ערך יחיד המשקף את מרכז הפצת הנתונים. יחד עם השונות
- נתונים נומינליים נתונים נומינליים בסטטיסטיקה, נתונים נומינליים (המכונים גם סולם נומינלי) הם סוג נתונים המשמש לתיוג משתנים מבלי לספק ערך כמותי כלשהו
- בדיקות לא-פרמטריות בדיקות לא-פרמטריות בסטטיסטיקה, מבחנים לא-פרמטריים הם שיטות ניתוח סטטיסטיות שאינן דורשות חלוקה כדי לעמוד בהנחות הנדרשות לניתוח.
- תנודתיות תנודתיות תנודתיות היא מדד לשיעור התנודות במחיר נייר ערך לאורך זמן. זה מציין את רמת הסיכון הקשורה לשינויים במחיר של נייר ערך. משקיעים וסוחרים מחשבים את התנודתיות של נייר ערך להערכת שינויים במחירים בעבר
